针对飞秒激光直写三维光子芯片的巨大应用潜力，研究团队提出并在芯片上成功验证了一种新型三维光子集成与操控机制−−非阿贝尔编织机制，用于实现片上光量子逻辑等应用。非阿贝尔编织的概念最早在凝聚态领域被提出，用于实现受拓扑保护的量子计算。非阿贝尔编织操作本质上是实现一个幺正矩阵变换，而矩阵中的相位因子可以用经典波体系的贝里几何相位构造，这给非阿贝尔编织在经典波中的实现和应用架起了桥梁。几何相位在光子学中早已获得了广泛的研究和应用（例如可以利用光学超表面来操控光子的偏转等特性），但这些研究中利用的贝里几何相位大多是一个相位因子，与之对应的具有非阿贝尔特性的贝里相位矩阵在光子学中仍未被广泛研究，其实现将为我们提供幺正矩阵等新的手段来操控光子，而这正是片上信息处理和运算所需要的重要功能。

    基于此，研究团队将非阿贝尔编织的概念引入到光子芯片中，首先给出在光子芯片上利用光波导结构实现2个光子模式编织的方案，该编织结构也会作为实现更多模式编织的基本单元。编织结构由4根单模光波导组成（图1a），其中波导A，B和S是不发生直接耦合的直波导，X是与三者耦合的弯曲波导。按功能划分，波导A和B是编织波导，波导S是储能波导，波导X是耦合波导，它与其它3个直波导的耦合系数如图1b所示。系统一共存在4个本征模式，受到手征对称性的保护，有2个模式从始至终保持简并状态，并保持和单波导结构具有相同的传播常数，而编织正是依靠这2个本征“零模”的绝热衍化实现的。整个编织过程，按照耦合系数的变化可以分为3个步骤：在步骤1中，依靠耦合系数的设计和2个简并零模的绝热衍化，从波导A入射的光子会绝热传输到波导S并获得一个π的几何相位（用A→-S表示，下同），而从波导B入射的光子保持位置不变（图1c）；步骤2的过程可以用B→-A和S→S描述；步骤3的结果为S→-B和A→A。由于在编织过程中光子只会分布在3根直波导中（提供耦合作用的X波导中始终没有光子），两组衍化过程中积累的动力学相位严格一致，因此整个编织过程可以用来描述（图1d，[]T中的项依次对应波导A和B中的波函数），其中由编织过程中几何相位积累组成的贝里相位矩阵，该矩阵对应量子逻辑Y门。

    研究团队利用飞秒激光直写技术在玻璃芯片中制备了上述结构，通过测试输出光在波导阵列中的分布，验证了2个光子模式的编织现象，即光子的输出波导与输入波导不同（图1e,f）；并通过设计一个干涉实验，证实了该编织过程的贝里几何相位矩阵（图2）。

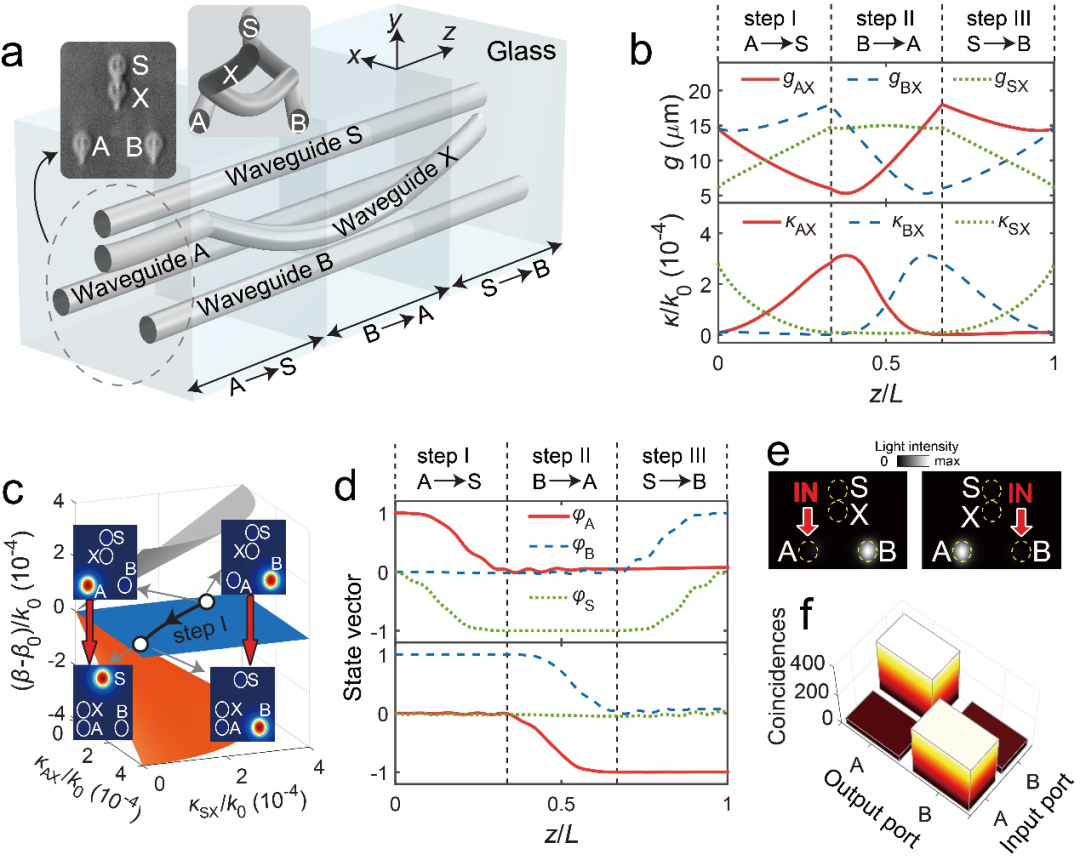
图1 飞秒激光直写光子芯片中实现2个光子模式的编织操作

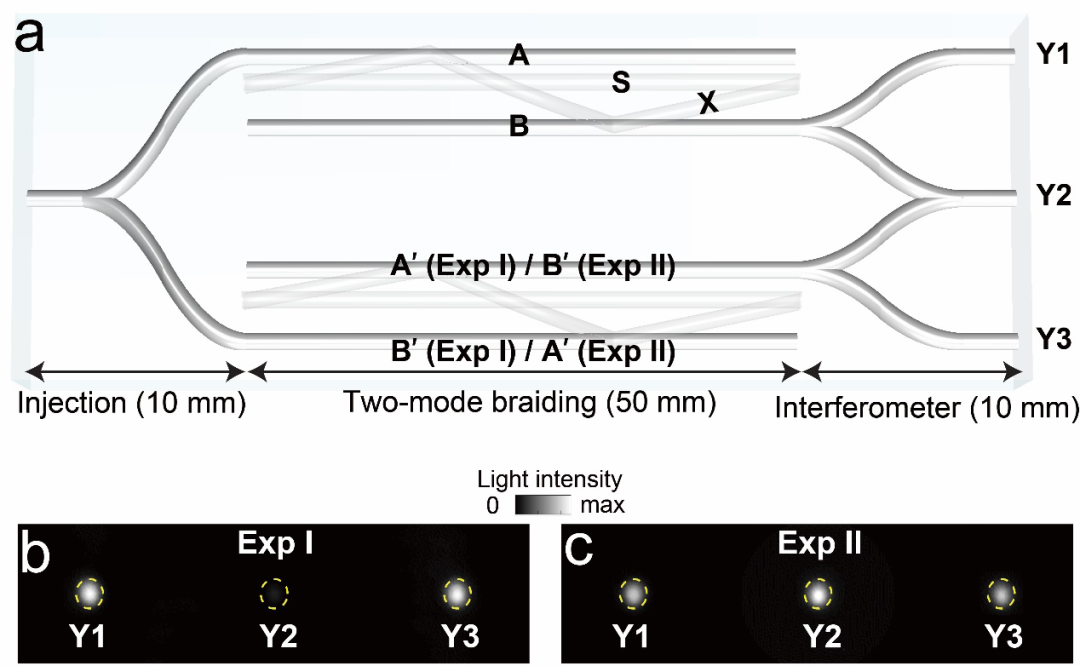
图2 编织过程中贝里几何相位的实验表征

    为了验证光子模式编织的非阿贝尔特性，研究团队通过在上述结构的基础上加入一组新的编织结构（包括编织波导C、耦合波导X2和储能波导S2），设计并制备了3个光子模式编织的结构（图3a）。研究人员定义了两个编织过程：G1编织过程实现波导A和B的编织而隔离波导C，G2编织过程实现波导B和C的编织而隔离波导A（图3b）。根据这两个编织过程的不同顺序组合，可以实现多种多样的编织操作。考虑G2G1（定义为先G1再G2，下同）和G1G2这两个编织操作，在相同的波函数输入下，这两个过程的输出分别为和。这说明编织结果依赖于编织顺序，即光子模式的编织操作具有非阿贝尔特性，这些特性在实验上被证实（图3c-f）。而非阿贝尔编织的另一个重要特性GiGi+1Gi = Gi+1GiGi+1也在实验上被成功表征。

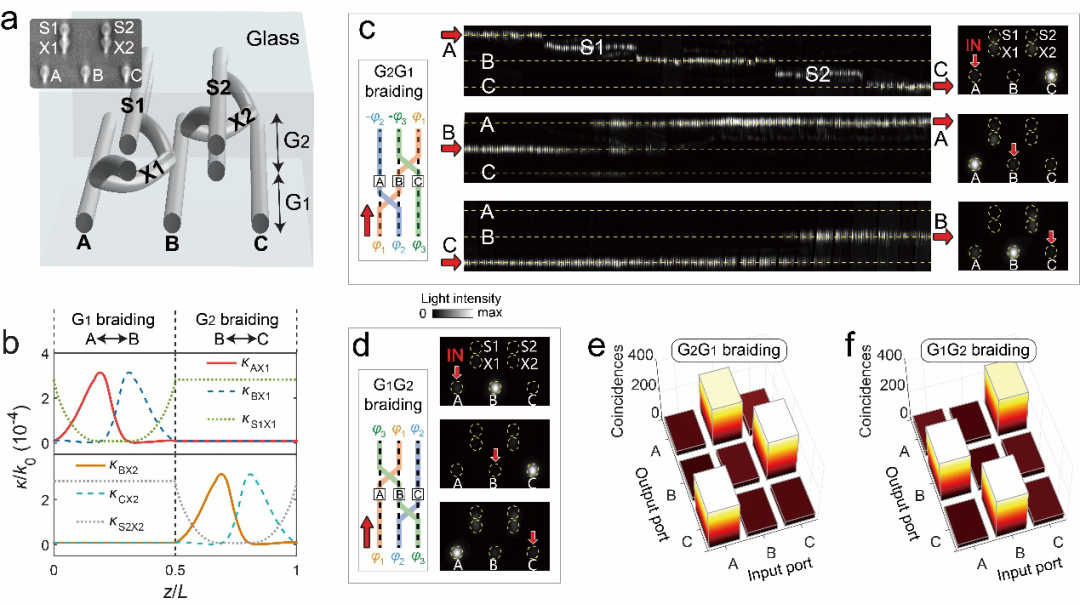
图3 飞秒激光直写光子芯片中实现三个光子模式的非阿贝尔编织

    基于飞秒激光直写技术制备的非阿贝尔编织器件具有良好的可拓展性，只需按照一定步骤直写新的编织波导、耦合波导和储能波导，就可以实现任意多个光子模式的编织操作（图4a），而通过设计具体的编织步骤可以构造丰富的贝里相位矩阵，用于量子逻辑等应用。作为展示，研究团队在实验上实现了5个光子模式的编织操作（图4b-e）。

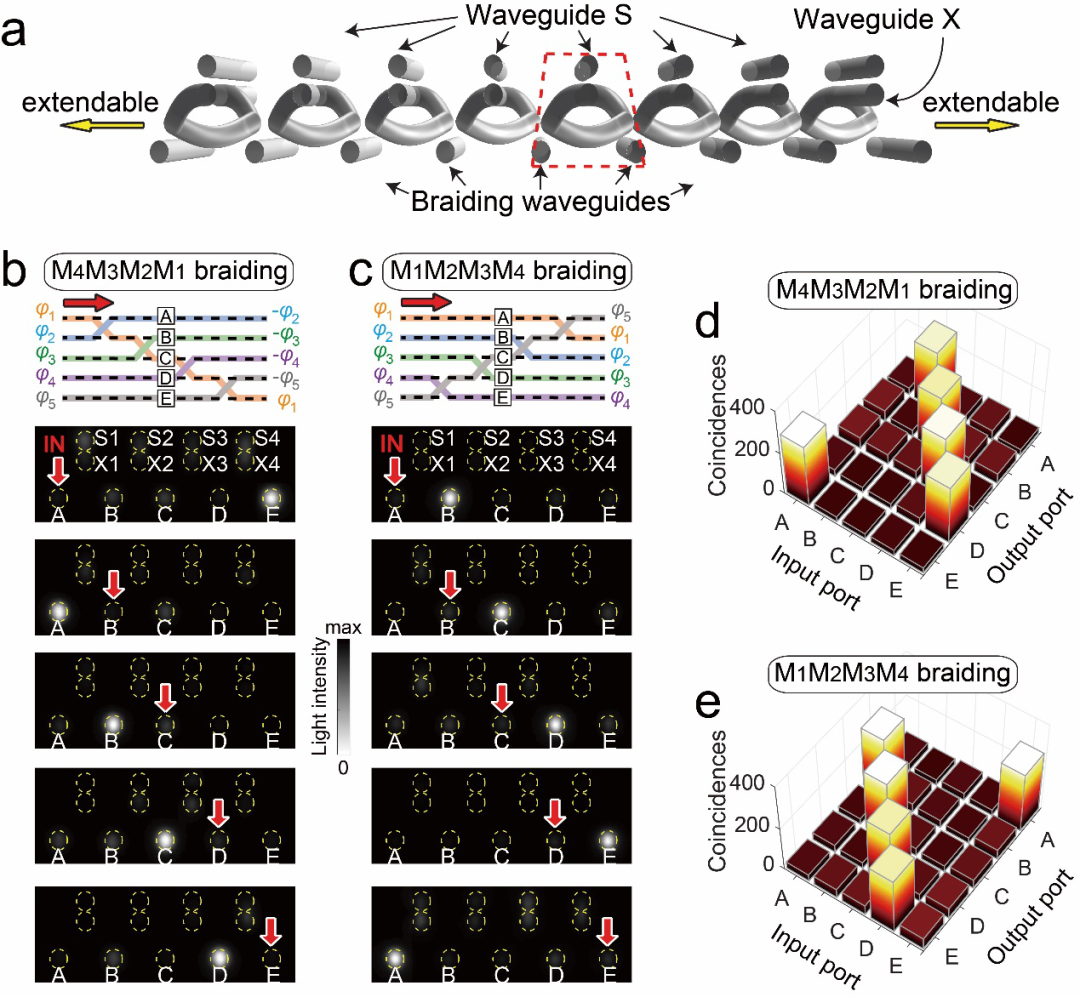
图4 非阿贝尔编织的可拓展性及5个光子模式的编织实验

以上内容来自光学工程。